오토마타 정리

기말 정리

시작 전에 간단한 정리

​

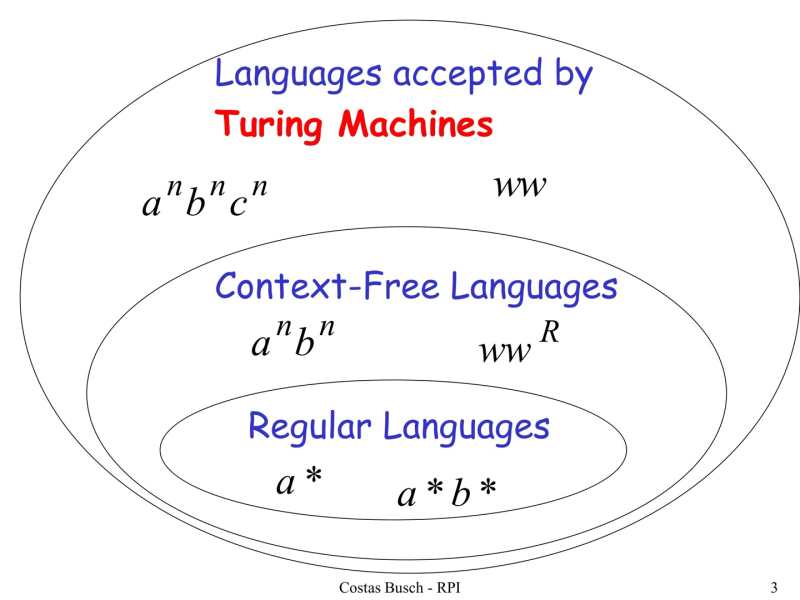
Regular - DFA, NFA

Context-Free - DPDA, (N)PDA

Context-Sensitive - lba(그냥 넘어감)

Recursively Enumerable - TM

​

​

​

Chap 6 : Simplifications of Context-Free Grammars

​

6.1 Methods for transforming grammars

• A substitution Rule(치환 규칙)
• Removing lambda productions

--> lambda 로 바로 가는 애들은 없애주고

--> Nullable variable을 다 찾고 그걸 포함하는 production에서 하나씩 다 치환

• Removing unit Productions

--> 위가 적용된 문법에서 시행

--> 만약에 S->B면 이 문법을 지우고, 대신 B가 만드는 걸 S에 추가시켜 주는 방식

• Removing Useless Production

1. string을 만들지 못하거나
2. 시작 변수에서 갈 수 없는 production

--> 찾으면 그와 관련된 모든 production을 제거

​

​

6.2 Normal Forms for Context-free Grammars

• Chomsky Normal Form(CNF)​​ --> CFG를 표기하는 방법 중 하나
• A -> BC or A -> a

--> 변수 -> 변수변수 or 변수 -> 심볼 ::: 딱 이 form이어야 CNF

• lambda production이 제거된 CFG는 무조건 CNF로 만들 수 있음

--> 어떻게 저떻게 잘 치환 해 봐

​

• Greinbach Normal Form (GNF)
• A -> aV1V2...Vk (k >= 0)

--> 첫번째거 무조건 심볼, 뒤부터 있으면 무조건 변수

• 마찬가지로, lambda production이 제거된 CFG는 무조건 GNF로 만들 수 있음

--> 어떻게 저떻게 잘 치환

​

​

6.3 Membership algorithm for CFG

• 어떤 스트링 w가 CFG에 포함 되냐의 문제
• CYK Algorithm ( O(w3) )

--> construct a Triangular Table

--> 어떻게 저떻게 잘 만들기.. V(1,length of w) 여기까지 오면 있는거임

​

​

​

Chapter 7: Pushdown Automata(PDA)

• CFL의 machine

​

7.1 Nondeterministic Pushdown Automata (NPDA)

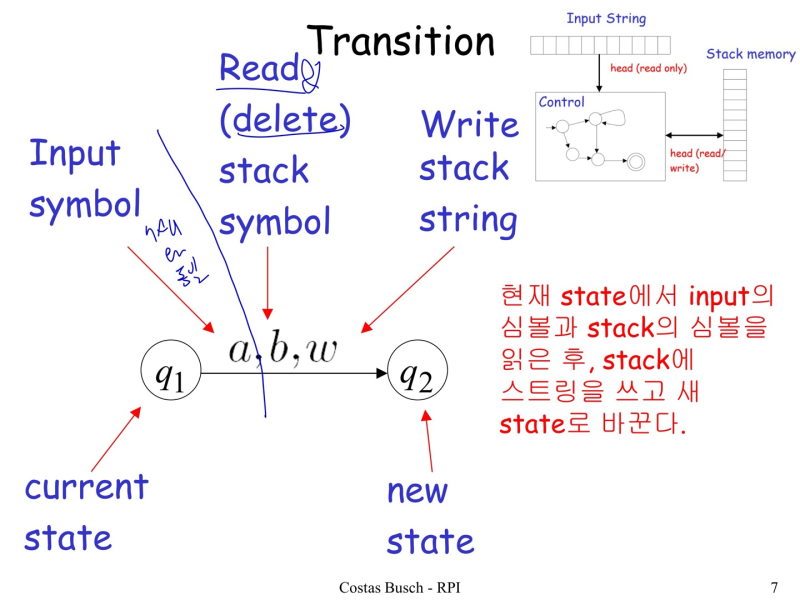
• input symbol 읽고, stack symbol 읽고 지우고, stack에 string 쓰고

--> 읽고, 쓰는건 하나씩 but stack에 쓸 string은 여러개일 수 있음 (c,d,f 면 f부터 stack에 write)

• Empty stack -> halt
• lambda transition 가능, multiple choices 가능
• 모든 input 다 읽고, last state가 final state일 때 accept

--> stack에 뭐가 남아있든 상관 ㄴㄴ

• 이 스트링에 대해서 accept 하는 길이 하나라도 있으면 accept
• NPDA 예시

 

​

• 순간묘사 (q, u, s)

--> (현재 state, 남은 input, 현재 stack)

​

7.2 PDA and Context-Free Languages

• CFL 이랑 NPDA 가 equivalent 한거 증명
• CFG --> NPDA

--> 일단 CFG를 GNF로 표기

--> 이 GNF를 leftmost derivation 하는 과정을 PDA가 simulation을 함

 

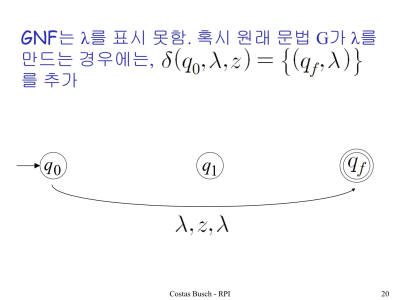
--> L(G) = L(M)

--> NPDA를 CFG로 만드는건 앞 과정의 역인데 훨씬 복잡하다고 한다 .. 생략하신다는데 과연 시험은 어떨지..

​

​

7.3 Deterministic PDA(DPDA)

• 공집합과 원소 1개인 집합만 허용(화살표 0개 or 1개)
• state q 와 stack top b 상황에서 input을 읽기 / 안 읽기 두 상황이 모두 존재할 수 x

** dfa와의 차이 : lambda transition 허용, 공집합 허용

--> 앞에서 본 L(M) = {anbn : n >= 0} 은 Dterministic CFL이다.

​

• NPDA Have More Power than DPDAs

--> DFA 는 NFA와 동등하지만, DPDA < NPDA

ex)

--> 책이 없음 ㅋㅋ 대충 구글링 해보니 아무튼 a가 b로 넘어갈 때 1개 할 지 2개할 지 그게 deterministic이 아니라서 이거로 만들 수가 없다 대충 이런 느낌인 듯

​

NPDA 예시

--> 중간점을 어케 앎? : nondeterministic 하게 모든 점을 다 체크해봄

​

​

Chapter 8 : Properties of Context-Free languages

​

8.1 Pumping Lemma for Context-Free Languages

--> 펌핑렘마는... 그냥 알아서 해보자

​

8.2 Closure Properties for context-free languages

• Union, Concatenation, Star Closure 다 됨
• L1 - CFL , L2 - CFL 일 때 , L1, L2의 교집합은 CFL 보장 X
• L이 CFL일 때 , L의 여집합은 CFL 보장 X

--> 여집합이 닫혀 있다고 가정하면, 교집합에 닫히게 되는데, 교집합이 보장 X라

​

• L1 - CFL, L2 - regular 일 때, L1, L2의 교집합은 CFL임

​

​

Chapter10 : Turing Machines(TM)

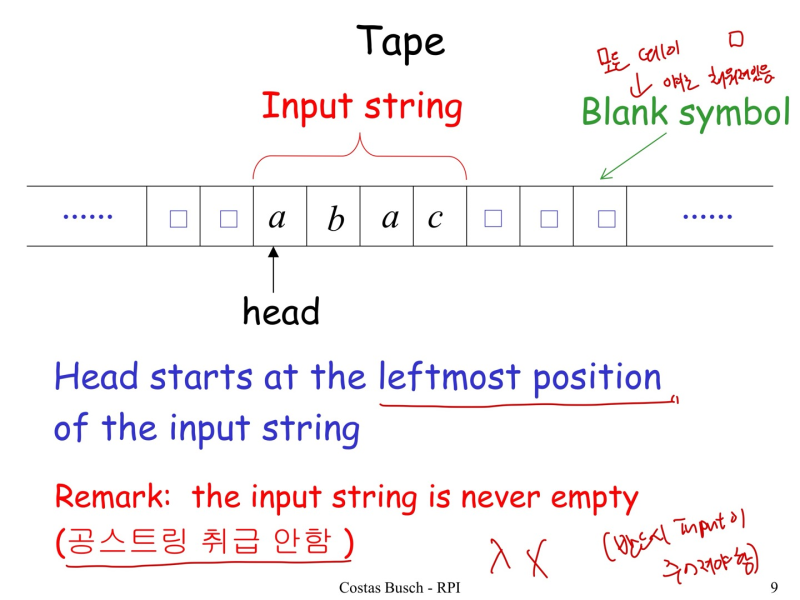
• 양방향 무한
• a(read), b(write), R or L (move)
• TM은 deterministic이다. --> multiple choice not allowed
• 아예 그 심볼에 대해 화살표가 안나가는건 허용 (이건 dfa만 허용 안한다)- partial function
• input symbol에 대해 가능한 transition이 없으면 HALT
• final state에서 HALT (final에서 나가는 화살표 있으면 안됨)
• reject 하는 경우 - final이 아닌 곳에서 halt 하거나, infinite loop에 들어간 경우
• final state에 들어가면 바로 전체 input을 accept(다 읽을 필요 x)

​

Computing function with Turing machines

• unary representation
• 컴퓨터로 할 수 있는 모든걸 TM으로 가능

--> Adder, copier, doubler, comparer, multiplier... 등등등

​

Decidable Properties of CFL => computable => 알고리즘 존재

​

9.2 Combining Turing machines for complicated tasks

• TM이 Transducer로서 활용

​

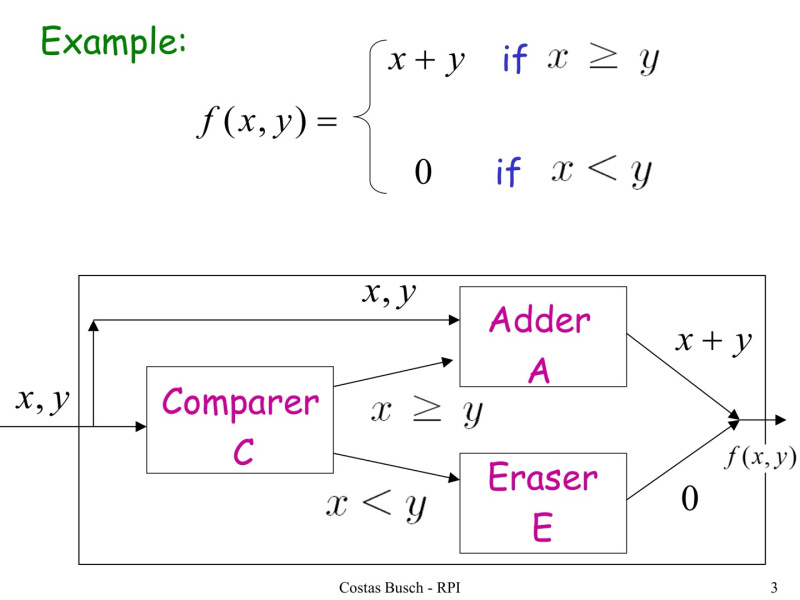
9.3 Turing's Thesis(가설)

• 어떤 기계적인 수단으로 할 수 있는 computation은 Turing Machine에서도 할 수 있다.
• Algorithms == Turing Machine

--> 알고리즘이 존재하면 그 알고리즘을 실행할 수 있는 TM 존재

​

Other Models of Turing Machine

• TMs with Stay

--> Left , Right 이외에도 Stay 할 수 있음

• TMs with a Multiple Track Tape

--> head 하나가 input 두개를 읽음

• Semi-Infinite Tape

--> 양방향 무한 아니고, 왼쪽 끝 존재

• The Off-Line Machine

--> input file 따로 존재

• Multi-tape Turing Machines

--> tape이 여러개 (head도 여러개, 독립적 작동)

• Two-Dimensional Turing Machines

--> head가 L,R 뿐만아니라 Up, Down도 가능, 2차원 Tape

​

==> 모든 변형 TM들은 다 standard와 equally powerful 함

​

​

10.3 Nondeterministic Turing Machines

• Nondeterministic Choice를 허락함
• accept 하는 길이 하나라도 존재하면 accept
• 모든 deterministic machine은 nondeterministic machine

--> 어쨌든 deter이든 nondeter이든 두 TM은 equivalent 하다

--> keeps track of all possible computations 하면서 non이 하는 걸 시뮬 할 수 있음

​

10.4 Universal Turing Machine

• Reprogrammable TM
• General-purposed TM
• Simulates any other Turing Machine

--> 어떤 TM M 과 w가 입력으로 주어지면 M이 w를 입력으로 해서 하는 일을 그대로 simulation

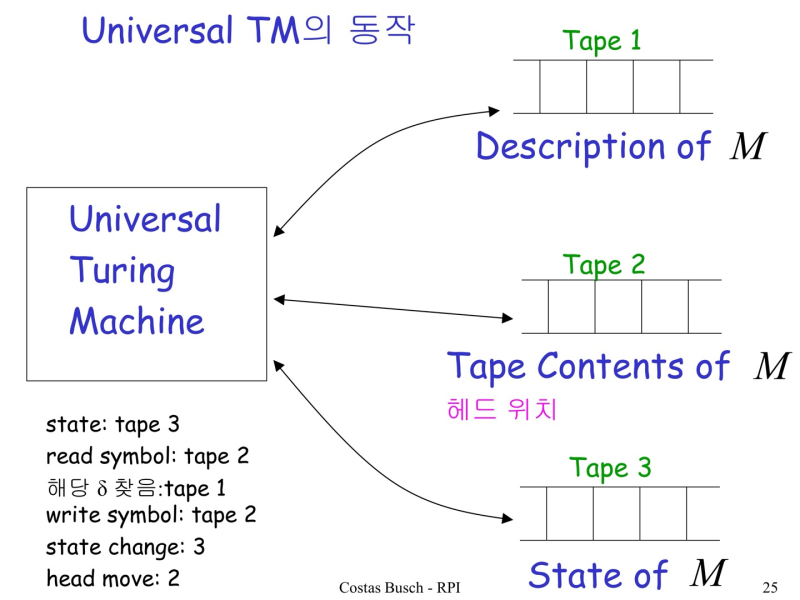
• tape 1 에 델타 함수 기록 => 어떻게?

=> M을 string으로 encoding 함

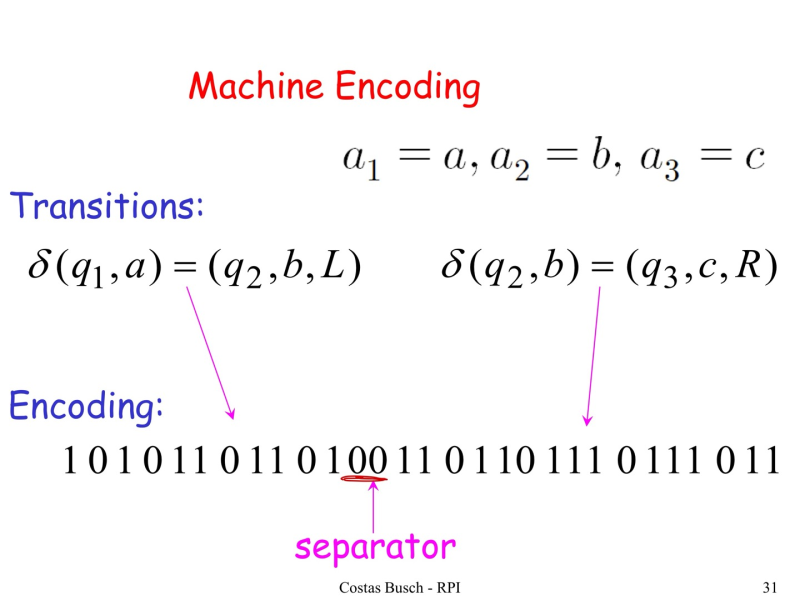
• The set of Turing machines forms a language

--> each string of the language is the binary encoding of a Turing machine

​

Set Theory

• Infinite sets은 countable or uncountable

--> countable : 모든 유한 집합, 정수 집합

--> uncountable : 실수 집합

• 각 element들을 양의 정수랑 1대1 매칭을 할 수 있으면 countable 하다고 함.

--> rational numbers(유리수) 는 countable

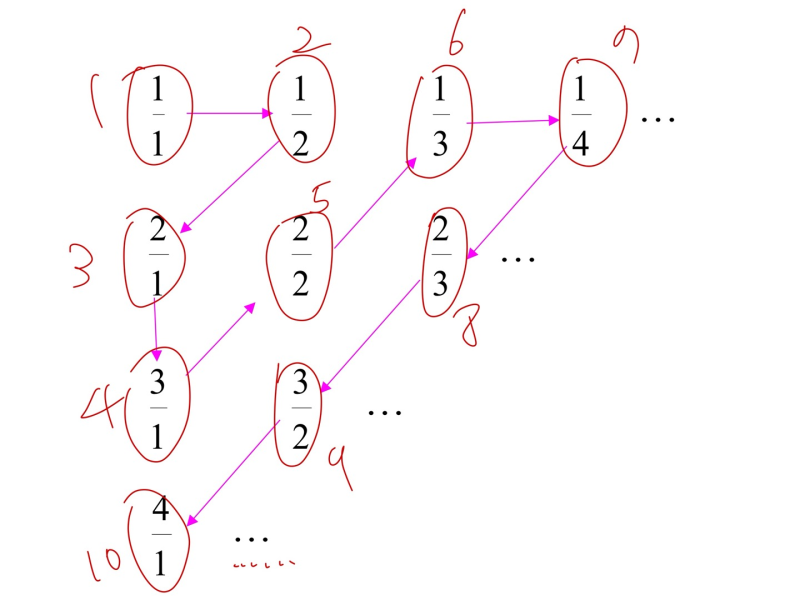
• 어떤 집합이 enumeration procedure이면, countable 하다
• {a, b, c}+ 는 countable

​

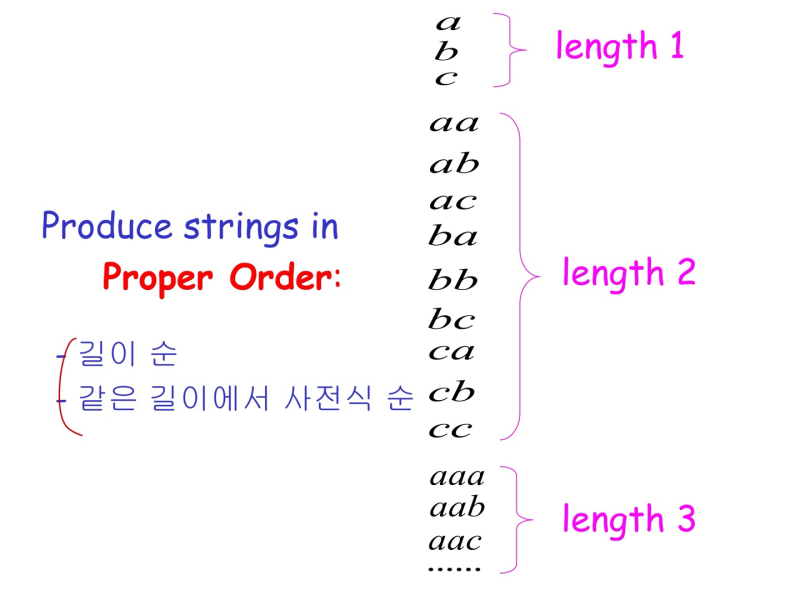
Enumeration Procedure:

• binary string을 무한으로 만듬 proper order를 해서
• 그렇게 만들어진 string이 위에서 본 encoding된 형식이면 output, 아니면 무시

​

​

Chapter 11: Hierarchy of Formal Languages and Automata

** recursive : always finishes 의미

--> 어떤 스트링이 그 L에 속하냐/ 안속하냐를 yes or no로 판단하는 알고리즘이 있으면 recursive

• 모든 CFL은 recursive L (Cyk 알고리즘 존재)

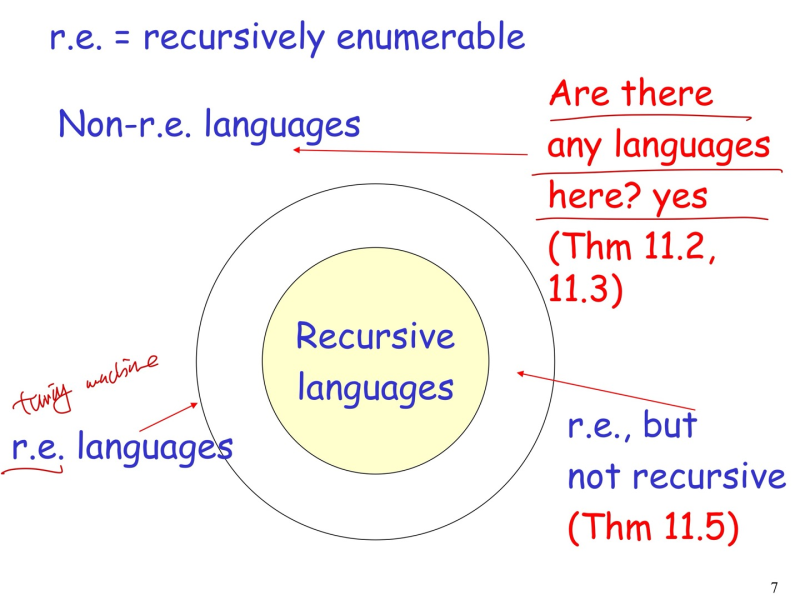
--> 아무튼 파워셋은 uncontable임

--> TM이 없는 language 존재

​

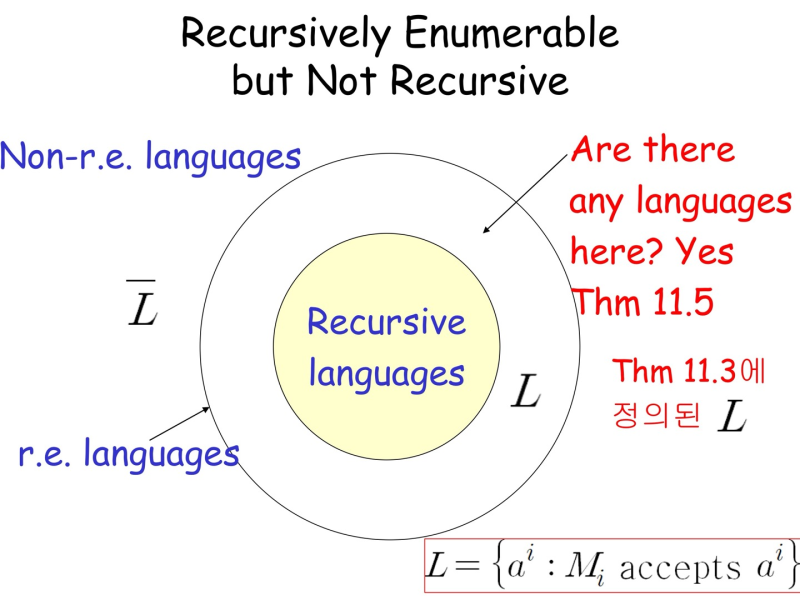
--> L 증명 생략(책에 있음)

​

11.2, 11.3

Unrestricted Grammar : 최상위 문법

== TMs, r.e. languages

​

Context-sensitive Grammar

• 모든 CSG는 recursive함

​

chapter 12 : Limits of Algorithmic computation

​

Halting Problem (HP)

• undecidable(unsolvable) problem

--> 어떤 TM이랑 w 이 주어졌을 때 이게 halt 할지, 안할지 알 수 있음? -> ㄴㄴ

• Is a cfg unambiguous?
• Are two cfg's equivalent?
• Do two cfg's generate any common string?

--> 일반적인 input에 대한 알고리즘 없음

​