Greedy - Prim Algorithm : MST

Prim Algorithm - Part 1.

Prim's Algorithm: node(vertex)-based approach(ranking)

F = empty set  // ouput => 조건에 맞는 edge들을 추가해감
Y = {v1} ==> start edge

while NOT solved yet{
	select v in V-Y nearest to Y # selection	
	feasibility test (cycle?) # 불필요 
    # => 이미 가지고 있는 node에서 짧게 연결되는 노드를 가져옴 => cycle이 생길 수가 없음 (가지고 있는 노드는 다음 loop에서 제외되니까 그런듯?)
	ADD v to Y
	if V == Y
    	stop/exit. 
}

 

 

 

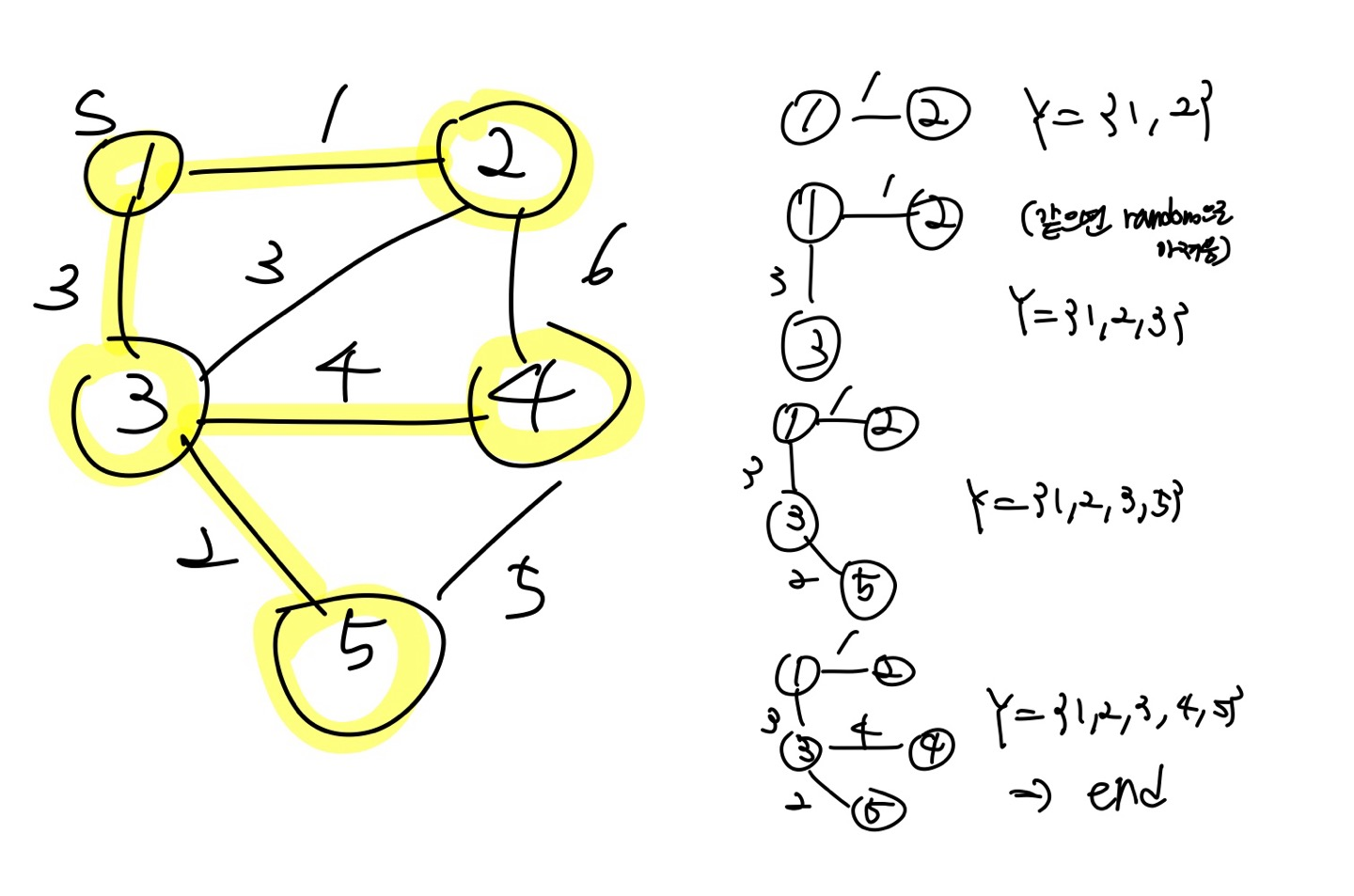
<Analysis>

1. Time complexity T(n)

=> Greedy? ==> LOC 에 따라 달라짐 => 알아서 계산

=> Prim = T(|V|) = T(n) ~=(n-1)(n-2) ~= O(n^2) 

(총 vertex 개수 = n 이라고 했을 때, start vertex 제외, n-1개의 vertex가 자신을 뺀 n-2개의 vertex를 확인하면서 loop)

2. LOC를 하는 과정에서 이게 과연 optimal minimum을 보장할 수 있나?
 => Proof required (반드시 proof 되어야 하는 건 아님)
  ( optimal이 아니어도 동작하는 greedy algo이긴하나, optimal인지  확인해보는 과정은 필요하다)

Prim Algorithm - Part 2.

Proof of Greedy Algorithm.

<Proof techniques>
Theorem, Axiom, Proposition, Predicates, ....... MIT MCS Lec1-3
Induction, Strong Induction, Proof by contradiction...
==> Induction을 가장 많이 사용한다고 함. (귀납법)

 

Prim's Theorem: "Prim's algo produces MST"
Proof: ............. by induction (greedy에 굉장히 많이 사용됨) => 왜? optimal => 다음 optimal ...

(Base) F = empty is promising. (MST를 만들어낸다...)
(H - 가설) Assume : F is promising(MST T = (Y,F)) 
(Induction) F + next dege (그 다음 생성되는 MST) is MST.

Proof on Induction is required ==> Lemma.  ( induction을 proof 하기 위해 소정리를 사용 )
=> technique: proof by contradiction

Contradiction: NOT F + next edge (그 다음 생성되는 MST) is MST.

==> induction을 반박하는 가설을 세워, 모순을 찾음 >>> 반박가설의 모순 == 원 가설이 맞음

T = (Y,F)

1) next tree: prim' algo. T(prim) = (Y+v, F+e) => MST X.

==> prim이 선택한 next vertex (v), next edge(e) 가 MST가 아니라는 것이 contradicion.

2) there exists another optimal MST : T(opt) = (Y+v', F+e') =>MST O

==> prim이 선택한 것이 MST가 아니라면, 또 다른 optimal MST가 존재한다는 소리가 된다

==> 즉, opt가 선택한 next vertex(v'), next edge(e') 가 MST가 되어야 한다.

===>위에서 설정한 내용을 다시 써보면, > T(opt = MST)이 T(Prim)보다 총 weight 합이 작다. < 는 뜻이 된다.
But, weight(T(opt))  >  weight(T(prim))
=> 왜? e' > e 

(애초에 Prim은 다음 edge에서 가장 작은걸 찾는 algo임. e'이 더 작았다면 prim은 e'을 선택했을 것이다.)  

==> Conflict!!!

 

즉, contratiction의 confilict가 발견되었으므로 Induction을 proof 할 수 있게 된다.