수정입니다
Memory Hierarchy(3) - Cache_2, Hamming code 본문
Associative Caches
- Fully associative
--> allow a given block to go in any cache entry
--> more flexible, reduce miss rate!!!
--> requires all entries to be serached at once
--> comparator per entry => expensive!
- M-way set associative (Fully 와 Direct map의 중간 지점)
--> Each set contains M entries
--> block number determines which set
(block number) % (number of sets in cache)
--> serch all entries in a given set at once
--> M comparators (less expensive)
Direct mapped vs Fully vs M-way
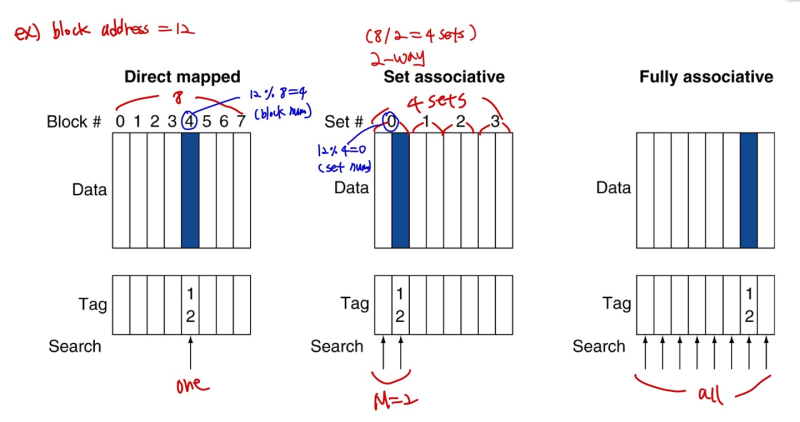
Spectrum of Associativity
- M-way에서 M = 1 --> Direct mapped
- M = number of blocks --> Fully associative
Associativity Example
- 귀찮으니 자료 첨부
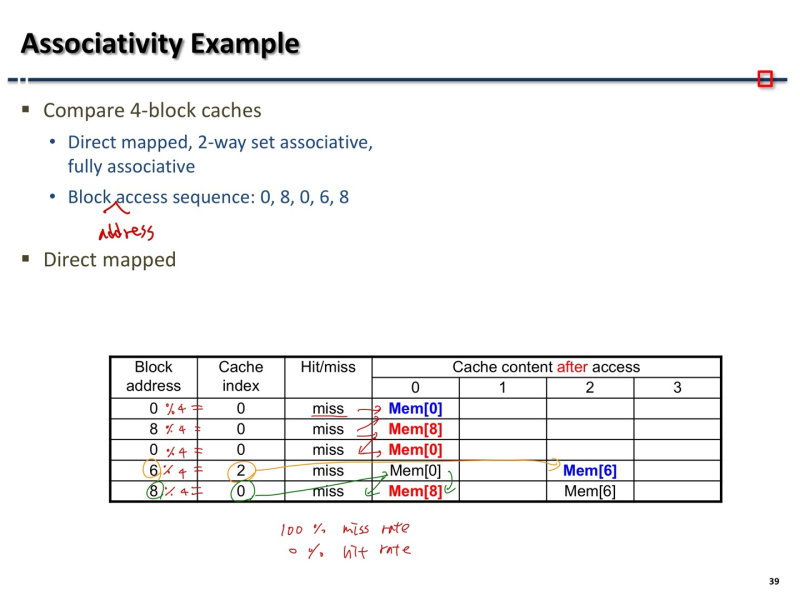
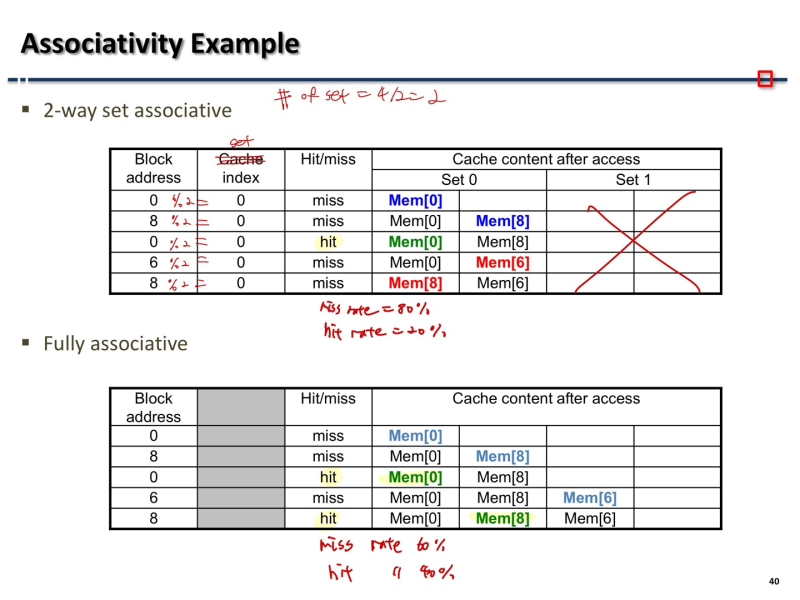
How much Associativity
- Increased associativity decreases miss rate
--> BUT with diminishing returns (M 을 계속 높일수록 퍼포먼스가 느는 퍼센트가 점점 줄어듬)
--> also, may increase search time or cost
--> 돈 많이 쓰고 miss를 줄일건지, 아끼고 miss를 감수할건지 선택
- Size of Tags versus set associativity
ex) 4096 blocks, 4-word block size, 32 bit addresses, what is the total number of tag bits?
공통 : 4-word block = 24byte/block -> byte offset : 4 bits
-> direct mapped
: 4096 = 212blocks -> index : 12 bits
: tag = 32 - 12 - 4 = 16 bits
: total number of tag bits = 212blocks * 16 bits = 216 bits = 64Kbits
-> 2-way associative
: number of sets = 212blocks / 2 = 211 sets -> index : 11 bits
: tag = 32 - 11 - 4 = 17 bits
: total number of tag bits = 212blocks * 17 bits = 69Kbits
-> 4-way accociative
: number of sets = 212blocks / 22 = 210 sets -> index : 10 bits
: tag = 32 - 10 - 4 = 18 bits
: total number of tag bits = 212blocks * 18 bits = 74Kbits
-> fully accociative
: index : 0
: tag = 32 - 4 = 28 bits
: total number of tag bits = 212blocks * 28 bits = 114Kbits
Set Associative Cache Organization
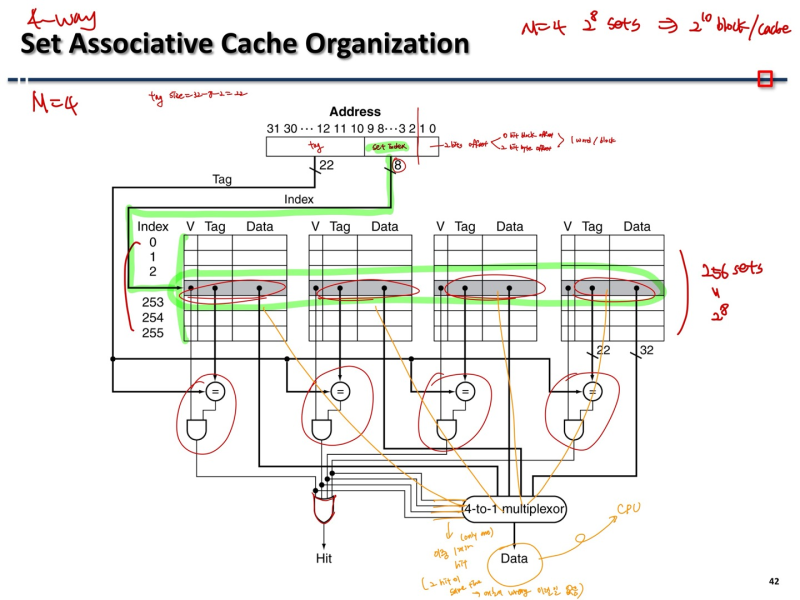
- 다 비슷한 원리..
- set들에서 온 값 들을 gate로 보내서 hit 된거 찾으면 됨4
Replacement Policy
- Direct mapped : no choice
- Set associative
--> 비어 있으면 쓰면되고
--> 다른 값이 들어있으면 set 안에 어떤 위치에 쓸 지 결정해야 함
- how?
--> Least-recently used(LRU)
: 오랫동안 안 쓴 값 기준으로 먼저 cache에서 내쫓는다(using 1 bit counter)
: 2 way는 쉽고, 4 way까진 관리할 수 있지만 그 이상은 힘들다(뭘 제일 안쓴건지도 다 비교해서 찾아야하니..)
--> Random
Multilevel Caches
- Primary cache attahed to CPU
--> small(비싸서), but fast
--> Focus on minimal hit time
- Level-2(L-2) cache
--> Larger(L1에 비해 상대적으로), slower, but 그래도 main memory 보다는 빠르다
--> Focus on low miss rate to avoid main memory access
Multilevel Cache Example(시험*********)
CPU base CPI = 1
clock rate = 4GHz
avg miss rate/instruction = 2%
main memory access time = 100ns
- With just primary cache
--> Miss penalty = main memory access time / clock period( or * clock rate)
= 100 ns / 0.25ns (or * 4GHz) = 400 cycles
--> Effective CPI = base CPI + avg miss rate/inst * miss penalty
= 1 + 0.02*400 = 9
- now add L-2 cache(access time = 5ns)
--> Global miss rate to main memory(CPU->L1->L2->main) = 0.5%
(L1->L2 : 25% of 2%, 전체에서 L2 miss 나는게 0.5%라는거고, L1에서 L2 miss 나는건 25%임(0.25*0.02 = 0.005)
primary miss with L2 hit
--> Penalty = 5ns / 0.25ns = 20 cycles
primary miss with L2 miss
--> Extra penalty = 400 cycles(cache 하나일 때 main 가는거랑 똑같은 이치)
--> Effective CPI = base CPI + L1 miss + L2 miss
= 1 + 0.02 * 20 + 0.005 * 400 = 3.4
- performance ratio = 9/3.4 = 2.6 times faster with L2 cache
Interactions with software
- misses depend on memory access patterns
--> algorithm behavior
--> compiler optimization for memory access
(한 위치에서의 캐시를 계속 계속 쓰는게 빠르지 계속 swap하면 miss 발생확률이 높아지고 느려진다)
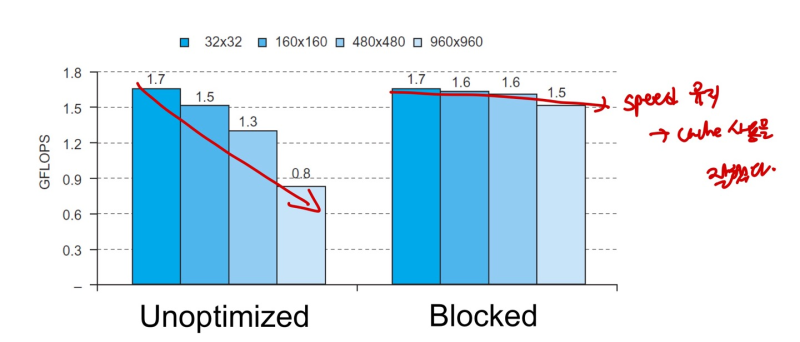
- Software Optimization via Blocking
--> Goal : maximize memory accesses to data before it is replaced (reduce cache replacement)
ex) DGEMM
--> matrix 계산을 매우 많이함 software에서
--> cache size는 매우 작기 때문에 이 많은 matrix 정보를 다 담아내지 못함
--> 그래서 matrix 계산할 때, cache에 적고 지우고하는 replacement를 매우 많이 하게 됨 :::: 느리다
--> IDEA : matrix 를 쪼개서 행렬곱을 최대한 많이 해놓고, 필요할 때 add해서 cache에 사용. (필요없으면 지움)
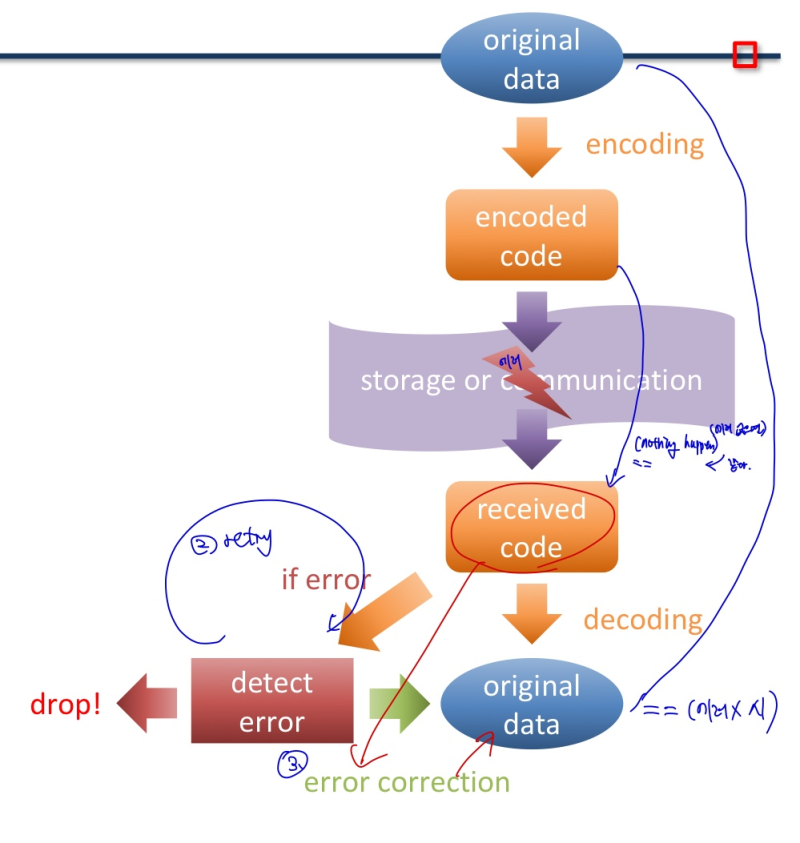
Encoding/Decoding
- 주로 error detection/correction 에 사용
- If error is detected
- may drop data (and maybe try again)
- may try to fix the error
The Hamming Code
- Hamming distance
--> Number of bits that are different between two bit patterns
(두 bit열의 같은 위치 비교, 서로 다른 bit 개수)
- [Minimum distance = 2]
--> single bit error detection
--> parity code
ex) 000111112 -> 0001111112 (오른쪽에서부터 비교하면, 파란색 부분이 서로 다름 -> distance 2)
--> original data에 1의 개수를 세서 odd 면 끝에 bit 1 추가, even이면 bit 0 추가
( encoding 된 data는 항상 1이 even number 임. 당연하지 홀수면 추가해서 짝수로 만들고 짝수면 0 붙였으니)
=> detect 1 bit error
=> but, cannot detect (2 bit, even, and distinguish 3 or more odd error)
- [Minimum distance = 3]
--> single error correction(SEC), 2 bit error detection(DED)
--> Hamming ECC code
Enconding Hamming SEC
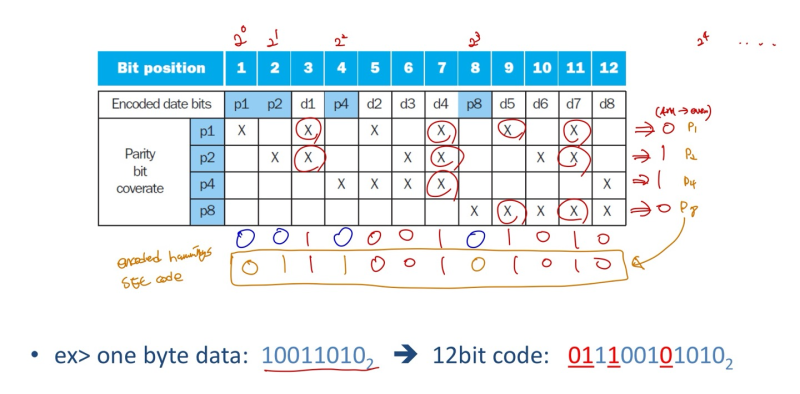
- parity bit p의 위치는 power 2 (20, 21, 22, 23 ...), 0으로 초기화 해놓는다
- 표시된 X를 보고 각 parity bit의 1의 개수를 체크해서, even 이면 0, odd 면 1을 setting
- 원래 위치에 바뀐 parity bit를 수정해서 넣어 encoding을 한다.
- p1 = 0, p2 = 1, p4 = 1, p8 = 0
Decoding Hamming SEC

- encoding 해서 받은 data를 다시 recalculated
- 똑같은 방식으로 1의 개수를 체크 -> 00002 면 no error
(encoding 할 때, odd 개수 였던 걸 다 even으로 맞춰줬으니, 문제가 없다면 다 even이어야 맞다)
- 만약, 11번 bit가 0으로 왔다고 해보자
--> 다시 1의 개수를 체크해보면 p1=1, p2=1, p4=0, p8=1로 홀수개가 껴있음을 알 수 있음
--> {p8, p4, p2, p1} = 10112 = 11 ---> 11번 bit에서 error가 났음을 확인할 수 있음 (고쳐주자)
- cost : original 8bit 였던 data를 comunication 할 때 12bit으로 만들어서, 50% 더 큰 데이터를 주고 받아야함.
** mark (X 표시) 하는 법
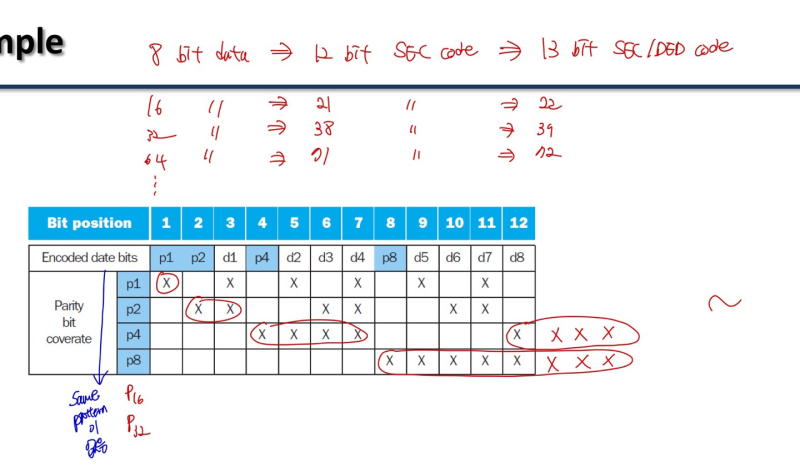
- 2의제곱수부터 그만큼의 간격, 그만큼의 X로 채워주기(그림 보면 감 올듯)
- parity bit를 추가해줘야 하기 때문에, orginal data가 가진 bit 내에서, 2의 제곱수 개수만큼 추가 bit 필요
--> 만약 19 bit data 라면, 19까지 2의 제곱수 5개(1,2,4,8,16) 의 추가 parity bit 필요 -> 24bit
Two - bit errors in Hamming SEC
- parity bit로는 딱 1bit error만 감지할 수 있다.
- 심지어 이게 1bit error인지 그 이상의 error인지도 구분을 못함
- 그 이상 error를 구분하고, 감지하려면 추가 bit 필요
SEC/DED Code (double - error detection code)
- add an additional parity bit 'pn' for the whole SEC code
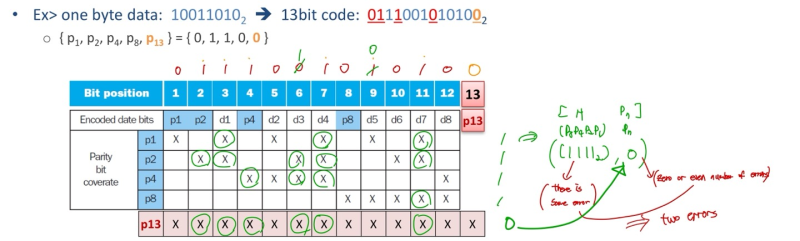
- SEC로 encoding된 bit 끝에 parity bit를 하나 더 추가
- 추가 parity bit는, SEC로 encoding된 bit열의 1의 개수를 세서 even이면 0, odd면 1
- 모든 bit에 X를 마크 해둔다
- Decoding : (H = SEC parity bits) = {p8, p4, p2, p1}
--> [H even(0000), pn even(0)] : no error
--> [H odd, pn odd(1)] : correctable single bit error
--> [H even(0000), pn odd(1)] : error in pn bit (추가 bit가 에러)
--> [H odd, pn even(0)] : double error occurred
'전공 > 컴퓨터구조' 카테고리의 다른 글
| Memory Hierarchy(4) - virtual memory (0) | 2023.12.28 |
|---|---|
| Memory Hierarchy(2) - Cache_1 (0) | 2023.12.28 |
| Memory Hierarchy(1) - Disk access time (0) | 2023.12.28 |
| Pipelining(2) (0) | 2023.12.28 |
| Pipelining(1) (1) | 2023.12.28 |



